The Power of Simplification: Unveiling the Karnaugh Map for Three Variables
Related Articles: The Power of Simplification: Unveiling the Karnaugh Map for Three Variables
Introduction
With enthusiasm, let’s navigate through the intriguing topic related to The Power of Simplification: Unveiling the Karnaugh Map for Three Variables. Let’s weave interesting information and offer fresh perspectives to the readers.
Table of Content
The Power of Simplification: Unveiling the Karnaugh Map for Three Variables
In the realm of digital logic design, the ability to simplify complex Boolean expressions is paramount. This simplification not only reduces the complexity of circuits but also enhances their efficiency and cost-effectiveness. A powerful tool for achieving this simplification is the Karnaugh map (K-map), a visual representation of Boolean functions that facilitates the identification and grouping of terms for simplification. While K-maps can be used for functions with any number of variables, this article delves into the specific application of K-maps for three-variable functions, highlighting their significance and practical utility.
Understanding the Essence of K-Maps
A K-map for three variables is a two-dimensional grid, essentially a visual representation of a truth table. Each cell in the grid corresponds to a unique combination of the three input variables. The arrangement of these cells is crucial, ensuring that adjacent cells differ by only a single variable. This arrangement facilitates the identification of adjacent cells representing "minterms" (product terms) that can be combined for simplification.
Constructing a K-Map for Three Variables
To construct a K-map for three variables, typically denoted as A, B, and C, follow these steps:
- Define the Grid: The K-map will have a 2×4 grid, with the rows representing the combinations of variables A and B, and the columns representing variable C.
- Label the Rows and Columns: Each row and column is labeled with the binary combinations of the corresponding variables. For instance, row 1 might represent A=0, B=0, while column 2 might represent C=1.
- Assign Cell Values: Each cell in the grid represents a unique combination of the three variables. The value of the cell is determined by the output of the Boolean function for that particular combination. A ‘1’ indicates a ‘true’ output, while a ‘0’ indicates a ‘false’ output.
Simplifying Boolean Expressions using K-Maps
The true power of K-maps lies in their ability to visually identify and combine adjacent cells representing minterms. These adjacent cells share all but one variable, allowing for the simplification of the corresponding product terms.
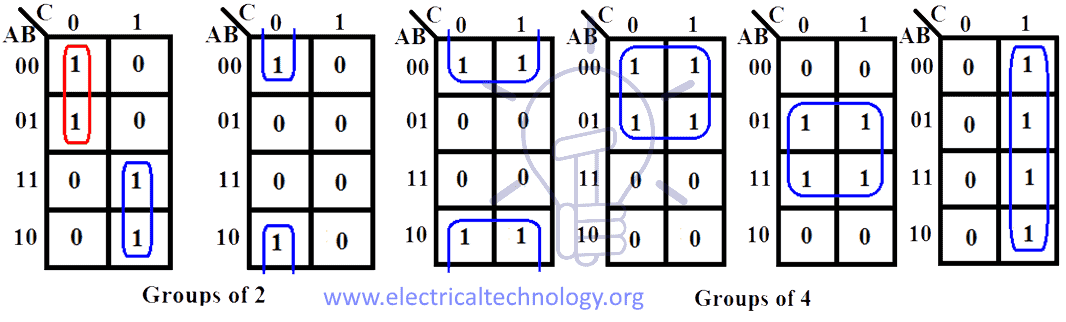
- Identify Groups of Ones: The goal is to group adjacent cells containing ‘1’s, forming rectangles or squares. These groups must have a power of 2 number of cells (1, 2, 4, 8, etc.).
- Find the Largest Groups: Prioritize forming the largest possible groups, as this leads to the most simplified expressions.
- Cover All Ones: Ensure that all cells containing ‘1’s are covered by at least one group.
- Write the Simplified Expression: For each group, identify the variable that remains constant across all cells within the group. This variable will be included in the simplified product term. Variables that change within the group are omitted.
Illustrative Example
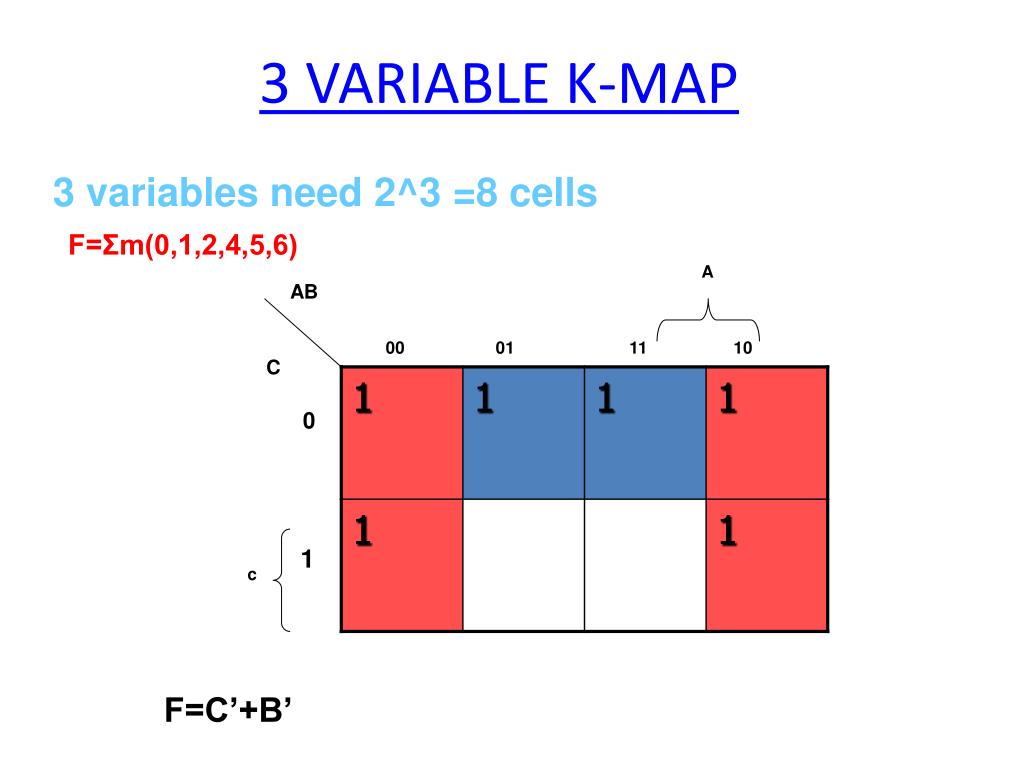
Let’s consider a Boolean function with three variables: F(A, B, C) = Σ(0, 1, 2, 4, 5, 7). This notation indicates that the function outputs ‘1’ for the minterms corresponding to decimal values 0, 1, 2, 4, 5, and 7.
-
Construct the K-map: The K-map for this function will have the following arrangement:
C=0 C=1 AB=00 AB=01 AB=11 AB=10 The cell values will be ‘1’ for the minterms corresponding to the given decimal values.
-
Identify Groups: We can form two groups: one covering cells 0, 1, 4, 5, and another covering cells 2, 7.
-
Write the Simplified Expression:
- Group 1: The variable C changes, while A and B remain constant at 0. Therefore, the simplified term is A’B’.
- Group 2: The variable A changes, while B and C remain constant at 1. Therefore, the simplified term is BC.
The final simplified expression for F(A, B, C) is: F(A, B, C) = A’B’ + BC
Significance of K-Maps in Digital Logic Design
The use of K-maps offers several significant benefits in digital logic design:
- Simplified Circuit Implementation: K-maps provide a systematic method to simplify Boolean expressions, resulting in circuits with fewer gates and reduced complexity. This leads to lower cost, smaller size, and increased reliability.
- Improved Circuit Performance: Simplifying Boolean expressions reduces the number of logic gates, resulting in faster signal propagation and reduced power consumption.
- Enhanced Design Efficiency: K-maps offer a visual approach to Boolean simplification, making the process intuitive and efficient. This allows designers to quickly identify optimal combinations and minimize design iterations.
FAQs Regarding Three-Variable K-Maps
Q1: Can a K-map be used for functions with more than three variables?
A: Yes, K-maps can be used for functions with any number of variables. However, for functions with more than three variables, the visual representation becomes more complex and requires additional techniques to handle the increased dimensionality.
Q2: How do I handle "don’t care" conditions in a K-map?
A: "Don’t care" conditions, denoted by ‘X’ in the K-map, represent input combinations that can be assigned either ‘0’ or ‘1’ without affecting the circuit’s functionality. These conditions can be used to simplify the expression further by including them in larger groups.
Q3: What are some limitations of K-maps?
A: While K-maps are a powerful tool, they become less efficient for functions with a large number of variables. In such cases, other methods like Quine-McCluskey algorithm might be more suitable.
Tips for Using K-Maps Effectively
- Understand the Grid Structure: Familiarize yourself with the arrangement of cells and the relationship between adjacent cells.
- Start with Small Groups: Begin by identifying smaller groups of ‘1’s and gradually expand them as needed.
- Prioritize the Largest Groups: Focus on forming the largest possible groups to achieve the most simplified expressions.
- Check for Don’t Cares: Utilize "don’t care" conditions to further simplify the expressions.
Conclusion
The Karnaugh map for three variables is a powerful tool for simplifying Boolean expressions and optimizing digital circuits. Its visual representation facilitates the identification of adjacent terms, allowing for efficient grouping and simplification. By leveraging the benefits of K-maps, designers can create more efficient, cost-effective, and reliable digital circuits. While K-maps have limitations for functions with a large number of variables, their simplicity and effectiveness make them an indispensable tool for digital logic design.
![[Blog Article] Three-Variable K-Map in SWITCHING THEORY AND LOGIC DESIGN , Lecture Notes](https://i.ytimg.com/vi/GuBVpgAVmDE/maxresdefault.jpg)






Closure
Thus, we hope this article has provided valuable insights into The Power of Simplification: Unveiling the Karnaugh Map for Three Variables. We appreciate your attention to our article. See you in our next article!